Если возникли проблемы при выполнении Задания 3.
вернуться на главную страницу можно, воспользовавшись ссылкой.

2.10. В связи с обнаружившимся непониманием, рассмотрим более подробно нахождение структуры базиса и ядра линейного оператора.

БАЗИС ОБРАЗА ОПЕРАТОРА - просто линейно-независимые столбцы матрицы оператора, их количество равно рангу матрицы оператора:

Проверить, принадлежит ли какой-либо вектор базису образа оператора означает проверить, линейно-зависим ли этот вектор от трех найденных вектор-столбцов (то есть увеличится ли ранг матрицы, образуемой найденными тремя вектор- столбцами и проверяемым вектором по сравнению с рангом матрицы А)

БАЗИС ЯДРА ОПЕРАТОРА - решения однородной системы уравнений (т.е. системы с правой частью - нулевым вектором), матрица которой является матрицей оператора. То есть системы Ax=0, где A - матрица оператора (для упрощения она берется сразу в ступенчатом виде, тем не менее, исходный вид, как известно, даст те же решения), x - вектор решений той же размерности, что и матрица.

Размерность пространства решений (т.е. количество л.н. векторов базиса) равна дефекту оператора, или n-r (где n-размерность матрицы оператора, r-ее ранг). (Ядро оператора - множество элементов, образом которых является 0-й элемент):

Проверить, принадлежит ли какой-либо вектор базису ядра оператора означает проверить, является ли он решением упомянутой однородной системы, т.е. будет ли результ перемножения матрицы А на этот вектор нулевым (как результат перемножения A на найденный вектор E1).

2.13. Скорее это не проблема, а вопрос: если при проверке выполнения задания вместо нулевых получаются значения, приведенные на рисунке - это не ошибка?Нет, не ошибка. Такие значения найденные MathCad значения в -14 степени - это в общем-то и есть нули при подсчете "с машинной точностью", так что все верно.
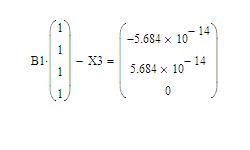